[Tutoriel] : comment créer un graphique « Radial Heat Map »
Dans cet article, nous allons créer un graphique un peu particulier qui fait partie de la famille des Special Charts : le Radial Heat Map Chart.
Son analyse est proche d’un graphe natif de Tableau la carte de chaleur ou Heat Map, à l’exception de sa forme circulaire qui permet :
- d’une part, une meilleure lisibilité dans le cas où les couples de modalités sont nombreux
- d’autre part, une touche d’originalité dans un dashboard.
Dans cet article, nous allons nous appuyer sur un business case dans le domaine pharmaceutique.
Un laboratoire pharmaceutique souhaite représenter sur une seule visualisation le niveau d’efficacité de 28 vaccins différents sur 5 virus. Pour cela, nous disposons de plusieurs données liées aux tests effectués notamment les champs suivants :
L’utilisation d’un Heat Map Chart semble être judicieuse, car elle offre la possibilité de représenter l’ensemble des couples Vaccins-Virus testés/non-testés. L’efficacité du vaccin, quant à elle pourrait être représentée par l’intensité de la couleur.
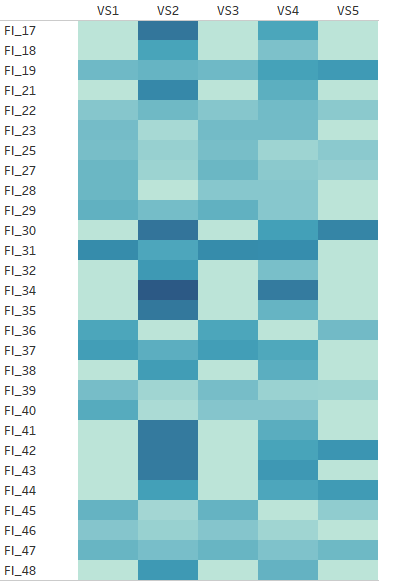Figure 1 : Heat Map Chart
NB : Pour obtenir cette représentation, il est nécessaire de remonter également les couples Vaccin-Virus non-testés en renseignant dans la source de données des valeurs nulles.
Cette représentation répond au besoin exprimé. Cependant, le nombre des modalités du couple Vaccin-Virus peut augmenter l’appréhension d’un utilisateur à analyser le graphe et rend la lisibilité plus difficile. Par ailleurs, un grand nombre de modalités implique l’utilisation de l’ascenseur afin d’observer tous les résultats.
Dans un soucis d’optimisation visuelle et analytique, l’utilisation du Radial Heat Map Chart peut être une solution de contournement de ces problématiques.
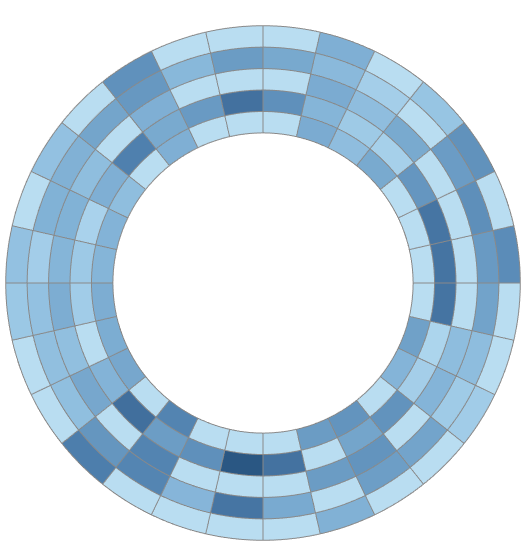Figure 2 : Radial Heat Map Chart
Le Radial Heap Map Chart permet d’avoir une vision d’ensemble des résultats et facilite la lecture mais également l’analyse du graphique.
I. Principe et rappels
1) Principe du Radial Heat Map Chart
Le Radial Heat Map Chart est un empilement de repères polygones définis par deux arcs de cercle et d’un angle agencés de la manière suivante :
Figure 3 : Rappels de géométrie
Pour cet exemple, le périmètre du polygone est un ensemble de 183 points ordonnés de la manière suivante :
Figure 4 : Définition d’un polygone pour le Radial Map Chart
Notons qu’un polygone est une forme géométrique fermée, c’est pour cela que le 1er et le 183ème point se superposent.
Afin d’obtenir les polygones, il est nécessaire d’associer les 183 points à chacune des modalités du couple Vaccin-Virus de la base de données. Pour ce faire, il suffit de créer un fichier de données « Point.csv » à une colonne dont les valeurs sont les valeurs ordonnées de 0 à 183. Ce fichier est ensuite joint avec la source de données principale à l’aide d’une clé fictive (1 = 1) créée dans chacune des sources de données.
2) Rappels mathématiques
Il est évident que le Radial Heat Map Chart est un Special Chart qui nécessite un peu de réflexion et de manipulation poussées. Pour le créer, nous allons devoir créer plusieurs champs calculés et pour ce faire nous plonger dans des souvenirs peut-être un peu lointains … Vous rappelez-vous des cours de trigonométrie au collège ?
Faisons un rapide petit rappel des notions de bases nécessaires pour comprendre la démarche suivie dans la suite de cet article.
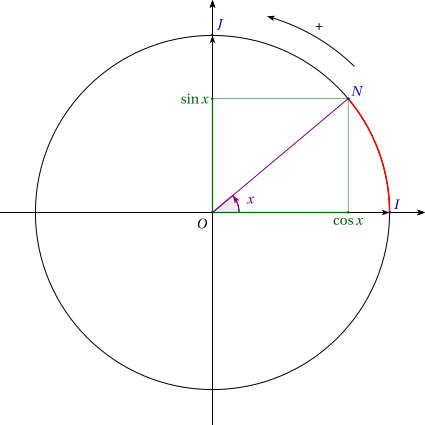
Figure 4 : Calculs trigonométriques
Cette première figure illustre le calcul de la position d’un point selon un angle x grâce au cosinus et au sinus de cet angle, où :
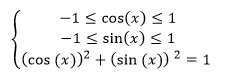
La dernière équation correspond au théorème de Pythagore et signifie que le rayon du cercle trigonométrique est égal à 1.
Par ailleurs, il est important de noter que le sens trigonométrique se fait dans le sens inverse des aiguilles d’une montre.
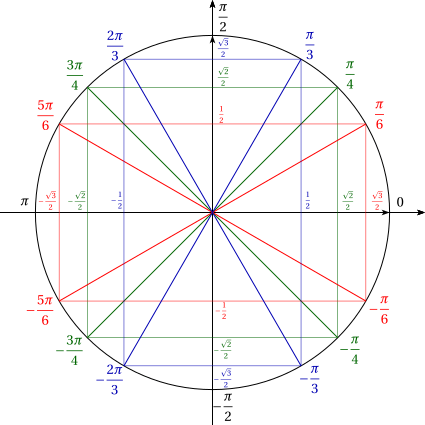
Figure 4 : Cercle trigonomértique en radian
Cette seconde figure illustre la mesure trigonométrique d’un cercle, la mesure π représente 180°.
Pour créer un Radial Heat Map Chart, nous allons créer des polygones en utilisant le repère polygone. Chaque polygone représente un couple Virus-Vaccin et son contour est composé, arbitrairement, de 183 points. 182 pour dessiner son contour, le 183ème ayant la même position de le 1er pour fermer la forme.
Pour placer chaque point sur la vue, il est nécessaire de définir le rayon et l’angle.
Trois champs calculés seront utilisés dans la vue, certains d’entre eux feront également appel à des champs calculés :
- X
- Y
- Color
II. Le champ [X]
Le champ [X] va représenter les valeurs en axe des abscisses, c’est-à-dire en Colonnes sur Tableau.
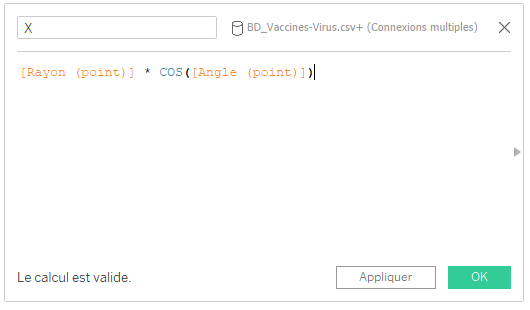
Par conséquent, la formule utilise un cosinus et est la suivante :
Tous les calculs imbriqués dans Rayon (point) et Rayon (point) lui-même sont calculés pour chaque Vaccin et pour tous les Virus.
Tous les calculs imbriqués dans Angle (point) et Angle (point) lui-même sont calculés pour chaque Virus et pour tous les Vaccins.
Une fois les champs calculés imbriqués créés, le champ calculé attendu est le suivant :
1) Le champ [Rayon (point)]
Le polygone possède visuellement 4 arrêtes principales : deux arcs de cercle de taille différentes et deux droites les reliant de même taille.
Les rayons des points du petit arc de cercle sont égaux, il en va de même pour les points formant le grand arc de cercle. Cependant, les rayons du petit arc de cercle et du grand arc de cercle ne sont pas égaux.
La formule du champ [Rayon (point)] permet de calculer la distance au centre de chaque point.
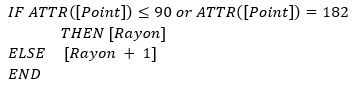
Le champ [Point] provient de la source de données et correspond au numéro des points formant le polygone. Pour rappel, ici, la forme est composée de 183 points, où
- Le petit arc de cercle est composé des points 0 à 90
- Le grand arc de cercle est composé des points 91 à 182
- Le point 183 correspond au même emplacement que le premier point permettant de fermer le polygone.
Ainsi, pour les points du petit arc de cercle, le rayon correspond à la valeur du champ [Rayon] et pour les points du grand arc de cercle, le rayon correspond à la valeur de [Rayon +1].
Une fois les champs calculés imbriqués créés, le champ calculé attendu est le suivant :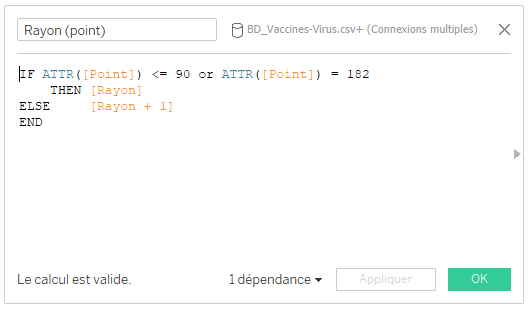
a. Le champ [Rayon]
Voici la formule utilisée pour calculer [Rayon] :
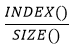
La fonction INDEX() retourne la position de la ligne dans la partition.
La fonction SIZE() retourne le nombre de lignes de la partition.
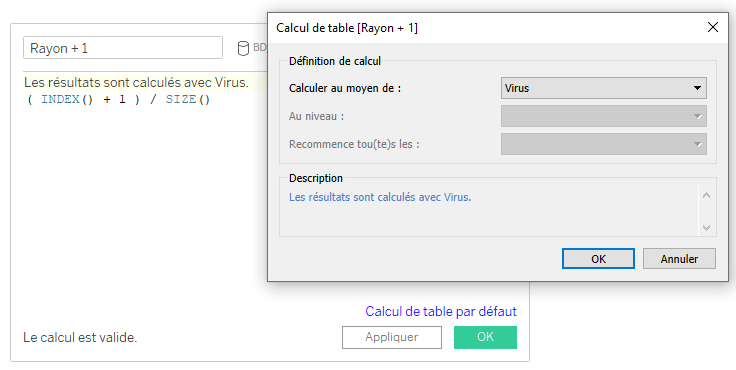
Attention, il est important de préciser par quel moyen le calcul de table est réalisé. Prenons un exemple avec le tableau croisé suivant :
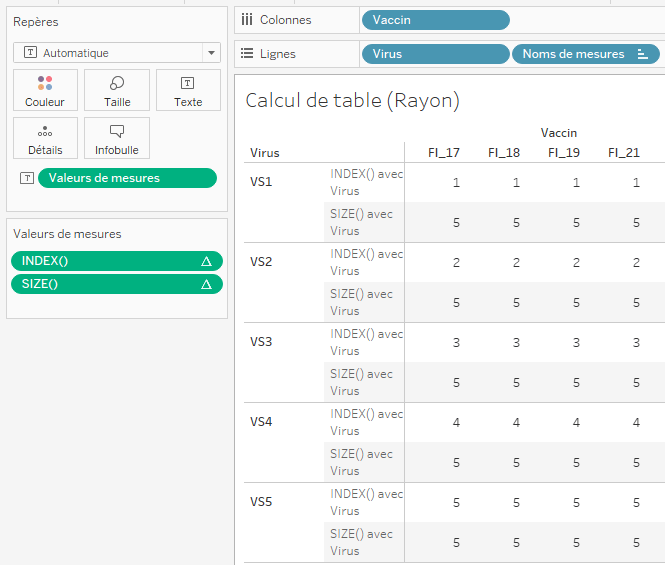
Ici, pour chaque Vaccin, nous obtenons la position de l’ensemble des Virus ainsi que la taille de la partition, c’est-à-dire le nombre de Virus testés par Vaccin.
Les deux calculs de table sont réalisés au moyen du champ [Virus], c’est-à-dire que pour chaque Vaccin et pour tous les Virus nous rechercons la position du Virus et la taille de la partition.
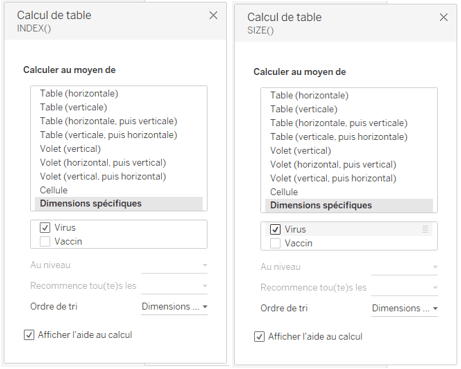
Le champ calculé attendu est le suivant :
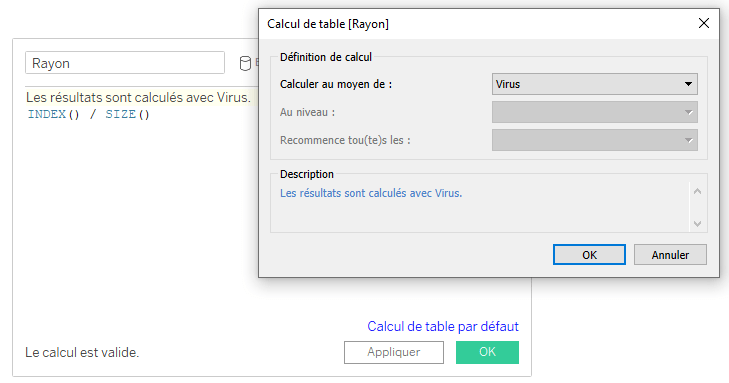
b. Le champ [Rayon + 1]
Voici la formule utilisée pour calculer [Rayon + 1] :
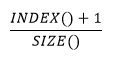
Le raisonnement du calcul de [Rayon + 1] est similaire à celui de [Rayon]. Il faut seulement ajouter 1 à la fonction INDEX() pour réaliser le calcul pour le grand arc de cercle.
Les deux calculs de table sont réalisés au moyen du champ [Virus], c’est-à-dire que pour chaque Vaccin et pour tous les Virus nous recherchons la position du Virus +1 et la taille de la partition.
Le champ calculé attendu est le suivant :
2) Le champ [Angle (point)]
Petit rappel, le polygone possède visuellement deux arcs de cercle de taille différentes. Les angles des points du petit arc de cercle sont égaux, il en va de même pour les points formant le grand arc de cercle. Mais leurs positions de départ ne sont pas les mêmes.
La formule Angle (point) permet de calculer l’angle formé pour chaque point ainsi que sa position dans le cercle.
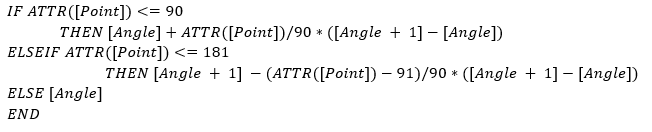
Le champ [Angle] correspond au positionnement du premier angle.
ATTR(Point)/X correspond à l’index du point divisé par la taille de l’arc de cercle obtenant ainsi le positionnement du point sur l’arc de cercle concerné.
[Angle +1] – [Angle] correspond à l’angle unitaire.
En tenant compte du sens trigonométrique et du positionnement des points vus dans la première partie de l’article (cf. Figure 4 : Calculs trigonométriques), le résultat de la première condition est une addition et celui de la seconde une soustraction.
Une fois les champs calculés imbriqués créés, le champ calculé attendu est le suivant :
a. Le champ [Angle]
Le champ [Angle] correspond à la taille de l’angle crée à partir de chaque point afin d’obtenir un cercle entier en les additionnant tous.
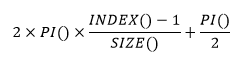
La formule 2π distribue le résultat sur toute la circonférence du cercle et non pas sur le 1er quart du cercle correspondant à l’intervalle [0 ; π/2] (le premier quart du cercle trigonométrique).
La lecture d’un cercle trigonométrique débute aux coordonnées (1,0) et se dirige dans le sens trigonométrique ou sens-inverse des aiguilles d’une montre. Par conséquent, pour faire correspondre le début de la lecture du graphe aux coordonnées (0,1), il faut décaler les valeur de +π/2 (cf. Figure 4 : Cercle trigonomértique en radian).
Soustraire 1 à l’index permet de faire débuter la lecture du graphe aux coordonnées (0,1), c’est-à-dire à 12h sur une horloge. La première valeur a pour INDEX() = 1, par conséquent en divisant par SIZE(), le point ne se retrouvera pas à 12h, mais sera décalé de 1/SIZE() dans le sens non-trigonométrique. Pour que la première valeur débute exactement aux coordonnées (0,1), il faut que INDEX() = 0, pour ce faire il faut soustraire 1 à INDEX().
Attention, il est important de préciser par quel moyen le calcul de table est réalisé. Prenons un exemple avec le tableau croisé suivant :
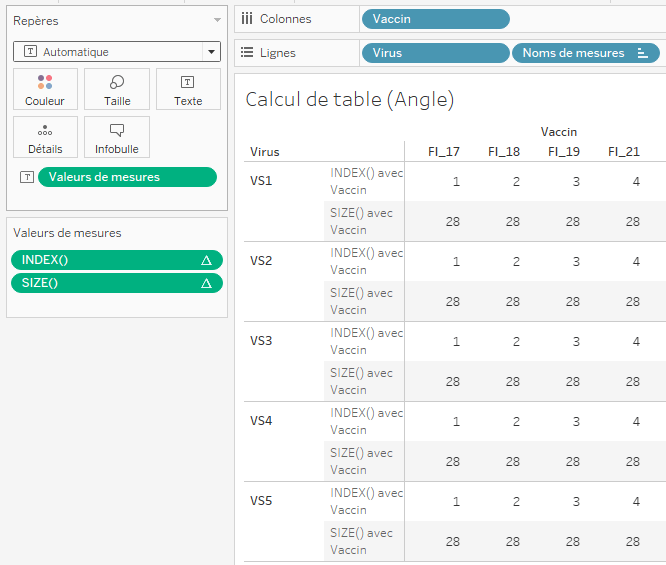
Ici, pour chaque virus, nous obtenons la position de chaque Vaccin ainsi que la taille de la partition, c’est-à-dire le nombre de Vaccin testés par Virus.
Les deux calculs de table sont réalisés au moyen du champ [Vaccin], c’est-à-dire que pour chaque Virus et pour tous les Vaccins nous recherchons la position du Vaccin – 1 et la taille de la partition.
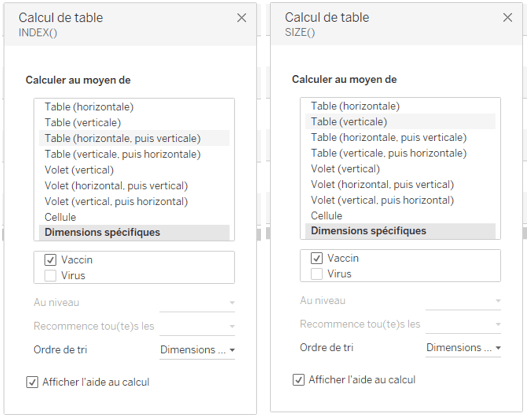
Le champ calculé attendu est le suivant :
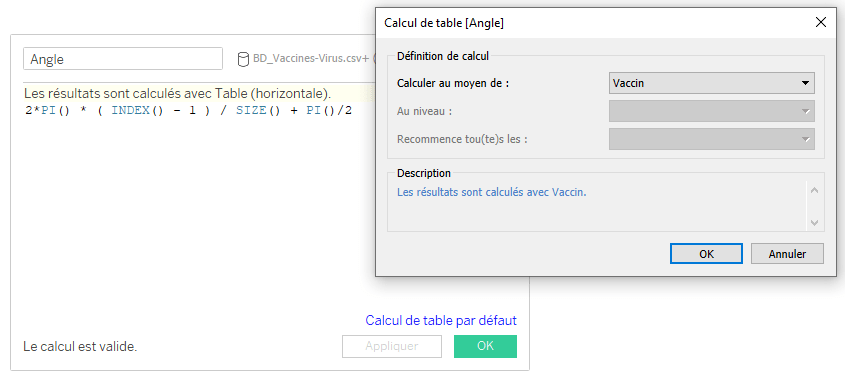
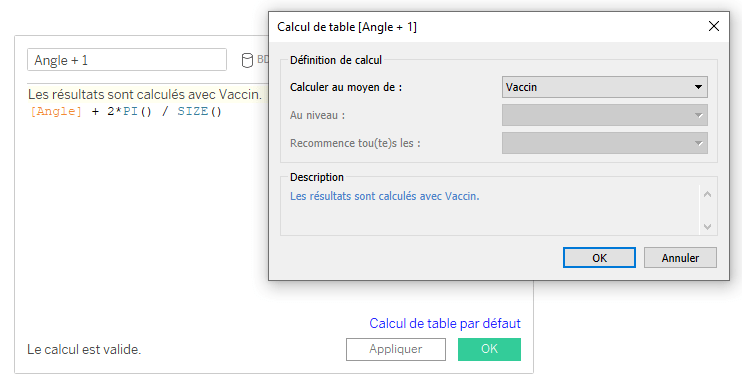
b. Le champ [Angle + 1]
Voici la formule utilisée pour calculer [Angle + 1] :
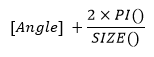
Le calcul des angles du grand arc se base sur le calcul de [Angle], vu juste au-dessus, auquel nous ajoutons la mesure de l’angle unitaire 2π/SIZE() où 2π représente la circonférence du cerle et SIZE() la taille de la partition, ici le nombre de vaccins.
Le calcul de table est réalisé au moyen du champ [Vaccin], c’est-à-dire que pour chaque Virus et pour tous les Vaccins nous recherchons la taille de la partition, le nombre de virus.
Le champ calculé attendu est le suivant :
III. Le champ [Y]
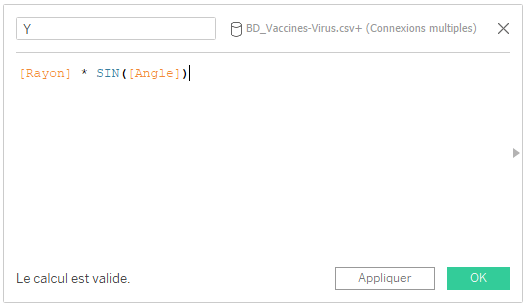
Le champ [Y] va représenter les valeurs en axe des ordonnées, c’est-à-dire en Lignes sur Tableau.
Par conséquent la formule utilise un sinus et est la suivante :
Les champs calculés [Rayon] et [Angle] sont les mêmes que pour le calcul du champ [X] et les champs calculés imbriqués le sont également.
Le champ calculé attendu est le suivant :
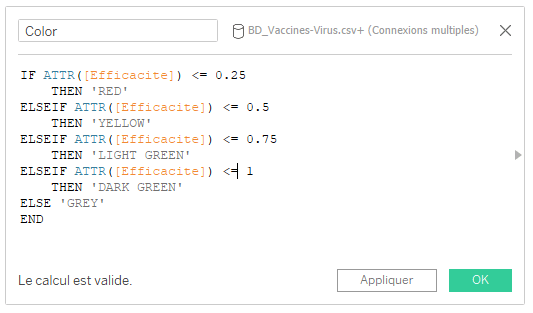
III. Le champ [Color]
Afin de représenter l’efficacité des vaccins selon le virus, il peut être intéressant d’ajouter une notion de couleur.
Voici le calcul proposé selon la valeur du champ [Efficacite] qui correspond à un scoring d’efficacité sur une échelle de 0 à 1.
IV. Construction du Radial Heat Map Chart
Reste maintenant à construire le graphe.
Pour ce faire, choisissons tout d’abord un type de repère Polygones.
Puis, il suffit d’ajouter sur l’étagère Colonnes le champ [X] et sur l’étagère Lignes le champ [Y], tous deux précédemment calculés et expliqués dans cet article.
Les deux champs [X] et [Y] sont en rouge. Tous deux contiennent des calculs de table nécessitant des granularités au niveau Vaccin et Virus, n’oublions pas de les renseigner dans l’étagères des repères en les glissant-déposant sur la boîte Détail.
Prenons bien garde à ce que les calculs de table imbriqués soit corrects en réalisant un clic droit sur chacune des pilules des champs [X] et [Y] et vérifiant que :
- pour les champs [Rayon] et [Rayon + 1], la dimension spécifique [Virus] est cochée
- pour les champs [Angle] et [Angle + 1], la dimension spécifique [Vaccin] est cochée
Glissons-déposons ensuite le champ [Color] dans l’étagère des repères sur la boîte Couleurs, où nous pouvons modifier les couleurs associées aux valeurs du champ [Color].
N’oublions pas de renseigner le Chemin dans l’étagère repère en glissant-déposant le champ [Point] pour indiquer l’ordre à suivre.
Enfin, pour plus de clarté, notamment pour les valeurs en gris, nous pouvons ajouter des bordures aux polygones tracés en cliquant sur la boîte Couleur de l’étagère repères et en sélectionnant l’affichage d’une bordure de la couleur de votre choix.
Et voilà ! 🙂
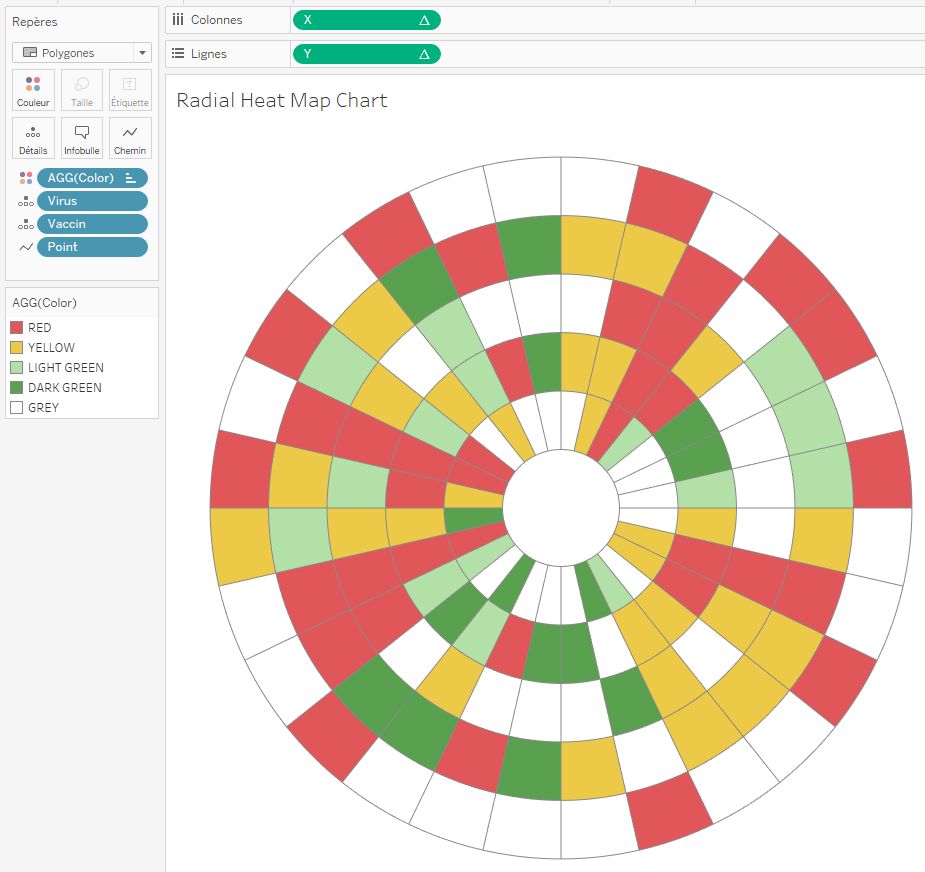
Figure 5 : Radial Heat Map Chart final
V. Pour aller plus loin
1) Modifier la taille du cercle intérieur
Si vous souhaitez que le centre de votre graphe soit un peu plus grand, il vous suffit de modifier légèrement les champs [Rayon] et [Rayon +1].
Dernier petit rappel, le cercle trigonométrique à un rayon de 1, il faut donc ajouter une valeur comprise dans l’intervalle [0 ; 1] et diviser proportionnellement INDEX() + 1 /SIZE().
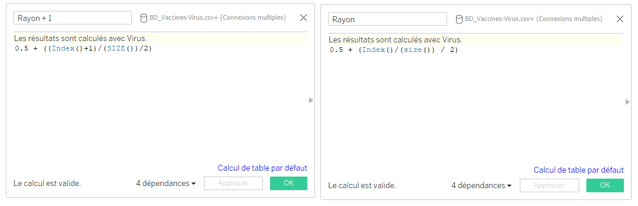
Ici, nous avons rajouté 0,5 et divisé par 2.
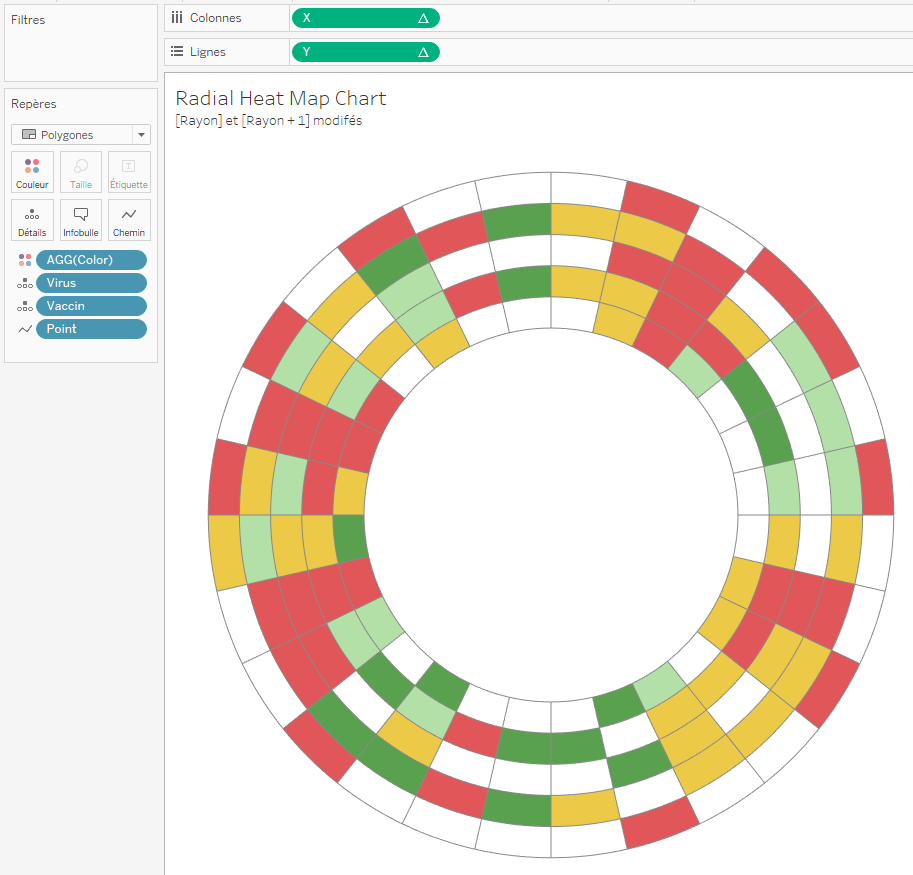
Figure 6 : Radial Heat Map Chart final amélioré
2) Ajouter les labels de vaccin et des virus
Pour plus de lisibilité, il serait intéressant d’ajouter des labels pour identifier les Vaccins et les Virus sur le graphe sans avoir à utiliser l’infobulle.
Pour ce faire poursuivez votre apprentissage via un second article Mydral sur le layering en suivant ce lien.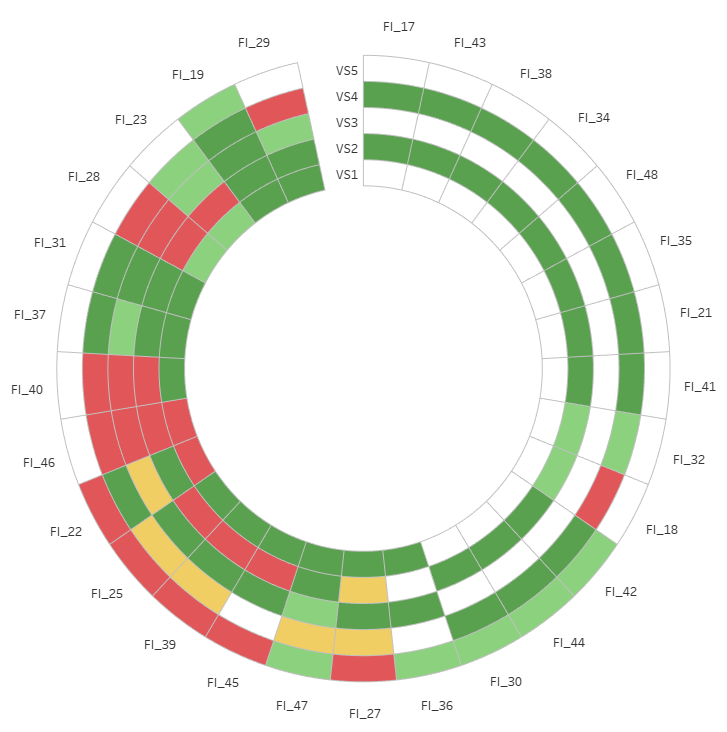
Figure 6 : Radial Heat Map Chart final avec les valeurs de Virus et Vaccin
Cet article sur la création d’un graphique Radial Heat Map Chart s’achève ici. N’hésitez pas à étoffer l’article en commentaire !
Le radial heat map chart n’a plus de secret pour vous ? Retrouvez d’autres tutoriels sur Tableau ici.
Suivez-nous sur les réseaux sociaux : LinkedIn & Twitter !
Author Profile
